نمودار تابع f(x)  بیانگر رفتار تابع f در دامنه اش است. مثلاً نمودار تابع f(x)=c  که یک تابع ثابت است، همواره به موازات محور x‌ هاست. با داشتن نمودار تابع می‌توان به برخی از خواص تابع پی برد.

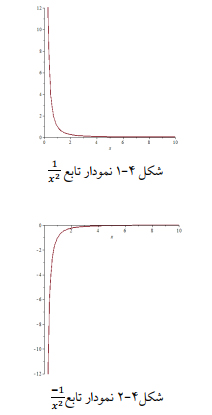
در بررسی نمودار توابعی که مجانب قائم دارند (مانند 1x2  یا -1x2  در نزدیکی صفر) نکته‌ای را می‌توان تداعی کرد به این ترتیب که در ازای تغییرات بسیار اندک متغیرx، تابع مقادیر بسیار بزرگ (به سوی بی‌نهایت) یا مقادیر بسیار کوچک (به سمت منهای بی‌نهایت) را اختیار می‌کند.

این مطلب ما را به یاد افرادی می‌اندازد که در یک مدت زمان کوتاه از نظر معنوی، حرکتی بسیار متعالی یا برعکس داشته‌اند. از جمله این افراد می‌توان حر بن یزید ریاحی را نام برد که وقتی به زمان ملاقات حر با امام حسین (ع) نزدیک می‌شویم، وضعیت معنوی حر به تعالی میل می‌کند (شبیه شاخه سمت راست نمودار تابع 1x2  وقتی که x به مبدا میل می‌کند).  یا می‌توان به بخشی از زندگی عمر سعد مراجعه نمود که در روز هشتم محرم سال 61 هجری قمری در ملاقات با امام بی‌احترامی و بی‌ادبی[1] نمود و این عمل سبب شد که وضعیت معنوی وی از روز هشتم محرم سال 61 هجری قمری اکیداً نزولی شود و زمانی که به روز دهم محرم سال 61 هجری قمری نزدیک می‌شویم، به سمت قهقرا (شبیه شاخه سمت راست نمودار تابع -1x2  وقتی که x به مبدأ میل می‌کند) میل کند.

مثال1: فرض کنید t زمان (واحد روز) و f(t)  تابع وضعیت معنوی در زمان t باشد. در صورت ثابت بودن این تابع، فرد مغبون خواهد شد. همان‌گونه که امام موسی کاظم A می‌فرمایند: آن کس که دو روزش (از نظر معنوی) مساوی باشد مغبون است[2].

تابع همانی: تابع همانی تابعی است مانند f  با ضابطۀ f(x)=x   که به هر x در دامنۀ f خود  x را نسبت می‌دهد.

استفاده از بحث گریز به جای این دیدگاه: به عنوان مثال تابع جزا که دامنه آن باطن اعمال انسان و برد آن جزای اعمال است، یک تابع همانی است. توضیح آن که هر عمل انسان در دنیا انجام می‌دهد یک ظاهر دارد و یک باطن. مثلاً باطن خوردن مال یتیم از روی ظلم، خوردن آتش است همانگونه که خداوند در قرآن کریم می‌فرمایند: «إِنَّ الَّذِینَ یأْكُلُونَ أَمْوَالَ الْیتَامَى ظُلْمًا إِنَّمَا یأْكُلُونَ فِی بُطُونِهِمْ نَارًا وَسَیصْلَوْنَ سَعِیرًا؛ [3] كسانی كه اموال یتیمان را از روی ظلم و ستم می‏خورند، تنها آتش می‏خورند و به زودی در شعله‏‌های آتش (دوزخ) می‏سوزند.»

البته انسانی که چشم بصیرت ندارد فقط ظاهر عمل را می‌بیند و باطن آن را نمی‌بیند در حالی که به محض انجام عمل، باطن ناری یا نوری آن ایجاد می‌شود، هر چند افراد درک نکنند. در قیامت با کنار رفتن پرده‌ها باطن عمل برای فرد آشکار می‌گردد. جزایی که انسان در قیامت دریافت می‌کند، عیناً باطن همان عملی است که در دنیا انجام داده است.

خدا در قرآن می‌فرماید: «هَلْ یجْزَوْنَ إِلَّا مَا كَانُوا یعْمَلُونَ؛ [4] آیا جز آنچه عمل می‌كردند به آن‌ها جزا داده می‌شود؟!»

تابع ثابت: تابعی است که به هر مقدار از دامنه، مقدار ثابتی را متناظر می‌کند. به عنوان مثال می‌توان تابع موت را که دامنه آن تمامی موجودات زنده و برد آن مرگ است، یک تابع ثابت دانست.

همانطور که قرآن می‌فرماید: «كُلُّ نَفْسٍ ذَائِقَةُ الْمَوْتِ؛ [5]هر كس مرگ را می‏چشد»

تابع اکیداً یکنوا: تابع f را اکیداً صعودی گوییم هرگاه به ازای هر x و y در دامنه تابع f، اگر x > y آنگاه f(x)>f(y)  به طور مشابه، تابع f را اکیداً نزولی گوییم هرگاه به ازای هر x و y در دامنه تابع f، اگر x > y آنگاه f(x)<f(y) . تابعی را که اکیداً صعودی یا اکیداً نزولی باشد را اکیداً یکنوا گوییم. به عنوان مثال اگرf تابعی با دامنه تعریف زمان باشد آنگاه در صورتی که با گذشت زمان مقدار تابع همواره افزایش پیدا کند آنگاه تابع اکیداً صعودی است و اگر با گذشت زمان مقدار تابع کاهش پیدا کند، آنگاه تابع اکیداً نزولی است.

مثال 1: هر چه عمر شخص بیشتر شود، فاصله او تا مرگ کمتر می‌شود. تابع f(x)=M-x  را که در آن x و M به ترتیب سن فعلی و سن در زمان مرگ فرد مشخصی است در نظر می‌گیریم. این تابع، تابعی اکیداً نزولی است[6].

گریز 1: انجام هر عمل صالح به شرط ایمان و اخلاص، باعث ارتقای مراتب معنوی فرد، می‌شود. به عبارت دیگر با افزایش تعداد اعمال صالح مقبول مثلاً تلاوت قرآن (با ایمان و اخلاص) مرتبه اخروی فرد ارتقا می‌یابد[7] همانگونه که ذکرخداوند (با ایمان و اخلاص) باعث ارتقای معنوی فرد می‌شود[8].

گریز2: در قرآن کریم خداوند متعال خطاب به حضرت رسول مکرم J می‌فرماید: «قُلْ رَبِّ زِدْنِی عِلْمًا؛ [9] بگو پروردگارا علم مرا افزون كن »

زیرا افزایش علم (منظور علمی است که با نیت و نگاه الهی تحصیل شود) باعث افزایش معرفت به خداوند می‌شود. بنابراین در اینجا افزایش معرفت به خداوند از افزایش علم تبعیت می‌کند.

گریز 3: عزت و محبوبیت، تابعی از طمع (چشم داشتن به دست دیگران) است. هر چه طمع شخص بیشتر شود، میزان عزت و محبوبیت او نزد دیگران کاهش می‌یابد.

تابع قدر مطلق: تابع f با ضابطه f(x)=|x|  را تابع قدرمطلق گویند. به عنوان مثال f(-2)=2,f(2)=2  یعنی تابع قدر مطلق، عدد منفی را به مثبت تبدیل می‌کند.

مثال 1: فرض کنیم x پسر جوانی باشد که تاکنون به مسافرت نرفته است و پس از رسیدن به سن تکلیف (15سالگی) nx  رکعت نماز خوانده وmx  رکعت نماز قضا دارد. اگر تعداد رکعت‌‌‌‌های خوانده شده را مثبت و خوانده نشده را منفی بگیریم، مطلوب است تعداد روزهایی که از رسیدن به سن تکلیف x گذشته است.

پاسخ: اگر تعداد رکعت‌‌‌‌های نمازهای واجب x را با  f(x) نشان دهیم داریم

f(x)=nx+|mx|

در این صورت تعداد روزهایی که از رسیدن این شخص به سن تکلیف می‌گذرد عبارت است از nx+|mx|17  اگر این کسر عدد صحیح باشد و در غیر این صورت برابر است با nx+|mx|17+1 .

برای مطالعه بیشتر:

از امام صادق A نقل می‌شود که حضرت فرمودند: «کسی که مراقبت بر وقت نماز خود نداشته باشد در روز قیامت خدا را ملاقات می‌کند در حالی که عهدی از خداوند بر گردن ندارد، (یعنی وعده‌‌‌‌های آمرزش خداوند شامل حال او نمی‌شود) اگر خداوند بخواهد او را عذاب می‌کند و اگر بخواهد او را مورد غفران قرار می‌دهد»[10].

در حدیث دیگری از ابو بصیر به نقل از امام صادق A بیان شده است که حضرت فرمودند: «اگر نماز در وقت خود ادا شود نماز فرد در حالی که نورانی است، ‌خطاب به وی بیان می‌دارد که تو مرا حفاظت کردی خدا تو را حافظ باشد اما اگر در غیر وقت نماز خوانده شود نماز خطاب به صاحب خود در حالی که مانند یک ابر تاریکی است بیان می‌دارد من را ضایع کردی خدا ضایعت کند»[11].

در حدیثی دیگر در همین باب بیان شده است که امام باقر A فرمودند: «پیامبر اکرم J در وقت مرگشان بیان داشتند از من نیستند دو گروه؛ یک دسته کسانی که نماز را سبک شمارند  و دسته دوم کسانی هستند که شراب و مست کننده می‌نوشند به خدا قسم این دو گروه بر سر حوض کوثر بر من وارد نمی‌شوند».[12]

برخی از احکام نماز قضا:

 کسی که نماز قضا دارد نباید در خواندن آن کوتاهی کند ولی واجب نیست فورا آن را بجا آورد.

کسی که چند نماز از او قضا شده و شماره آنها را نمی‌داند مثلا نمی‌داند چهار تا بوده یا پنج تا، چنانچه مقدار کمتر را بخواند کافی است و همچنین اگر شماره آنها را می‌دانسته و فراموش کرده، اگر مقدار کمتر را بخواند کفایت می‌کند.

کسی که نماز قضا از همین روز یا روزهای پیش دارد می‌تواند قبل از خواندن نمازی که قضا شده، نماز ادایی را بخواند و لازم نیست نماز قضا را جلو بیندازد.

 تا انسان زنده است اگر چه از خواندن نماز قضاهای خود عاجز باشد دیگری نمی‌تواند نمازهای او را قضا نماید.

 - نماز قضا را با جماعت می‌شود خواند، چه نماز امام جماعت ادا باشد یا قضا، و لازم نیست هر دو یک نماز را بخوانند مثلاً اگر نماز قضای صبح را با نماز ظهر یا عصر امام بخواند اشکال ندارد.

- مستحب است بچه ممیز یعنی بچه‌ای که خوب و بد را می‌فهمد به نماز خواندن و عبادت‌‌‌‌های دیگر عادت دهند بلکه مستحب است او را به قضای نمازها هم وادار نمایند.[13]

تابع چند ضابطه‌ای: بسیار اتفاق می‌افتد که مقدار تابع در سراسر دامنه‌اش با یک ضابطه مشخص نمی‌شود. مثلاً ممکن است دامنه تابع f که آن را X می‌نامیم را به n مجموعه Xn,...,X1 ، افراز کنیم و تابع f با دامنه X را برای هر x∈Xi  به صورت f(x)=fi(x)  تعریف کنیم که در آن fi  تابعی با دامنه Xi  است.

f(x)=f1(x)x∈X1f2(x)x∈X2⋮fn(x)x∈Xn

در این صورت تابعf  را n ضابطه‌ای گوییم.

مثال1: نمونه ساده‌ای از تابع چند ضابطه‌ای، تابع قدر مطلق است که قبلاً در مورد آن بحث شده است.

مثال2: خدا در قرآن می‌فرماید: «وَكُنْتُمْ أَزْوَاجًا ثَلَاثَةً فَأَصْحَابُ الْمَیمَنَةِ مَا أَصْحَابُ الْمَیمَنَةِ وَأَصْحَابُ الْمَشْأَمَةِ مَا أَصْحَابُ الْمَشْأَمَةِ وَالسَّابِقُونَ السَّابِقُونَ أُولَئِكَ الْمُقَرَّبُونَ [14]؛ و شما به سه گروه تقسیم خواهید شد نخست «اصحاب میمنه» هستند، چه اصحاب میمنه‏‌ای گروه دیگر اصحاب شومند، چه اصحاب شومی و سومین گروه پیشگامان پیشگام! آن‌ها مقربانند. »[15]

در ادامه آیات وضع حال این سه گروه توصیف می‌شود. اکنون اگر مجموعه X را مجموعه همه انسان‌ها در قیامت در نظر بگیریم، در این صورت X را می‌توان به سه دسته افراز نمود. مجموعه X1  مقربان درگاه، مجموعه X2  اصحاب یمین و مجموعه X3  اصحاب شمال. در این صورت تابع سه ضابطه‌ای f(x)  را می‌توان این‌چنین تعریف نمود:

همانگونه که خداوند در قرآن می‌فرمایند: «فَأَمَّا إِنْ كَانَ مِنَ الْمُقَرَّبِینَ فَرَوْحٌ وَرَیحَانٌ وَجَنَّتُ نَعِیمٍ وَأَمَّا إِنْ كَانَ مِنْ أَصْحَابِ الْیمِینِ فَسَلَامٌ لَكَ مِنْ أَصْحَابِ الْیمِینِ وَأَمَّا إِنْ كَانَ مِنَ الْمُكَذِّبِینَ الضَّالِّینَ فَنُزُلٌ مِنْ حَمِیمٍ وَتَصْلِیةُ جَحِیمٍ[16]؛ اما اگر او از مقربان باشد، در روح و ریحان و بهشت پرنعمت است اما اگر از اصحاب یمین باشد، به او گفته می‏شود: سلام بر تو از سوی دوستانت كه از اصحاب الیمین هستند اما اگر او از تكذیب كنندگان گمراه باشد، با آب جوشان دوزخ از او پذیرائی می‏شود! سپس سرنوشت او ورود در آتش جهنم است.»

در تابع سه ضابطه‌ای f(x)  می‌توان f1(x)  را  بهشت مقربان و f2(x)  را بهشت اصحاب شمال و نیز f3(x)  را جهنم، در نظر گرفت.

مثال3: همانگونه که در تفسیر برخی از آیات قرآن[17] آمده است، اگر t زمان باشد و fx  تابع زندگی فرد x باشد در این صورت تابع fx(t)  را می‌توان به صورت یک تابع دو ضابطه‌ای تعریف نمود:

fx(t)=&f1(t),t∈T1&f2(t),t∈T2

که در آن T1  زمان قبل از قیامت، T2  زمان بعد از قیامت، f1(t)  پنهان بودن باطن دل فرد x در زمان t و f2(t)   آشکار شدن باطن دل فرد x در زمان t است.

fxt=&1        x€X    0  &درغیر این صورت مثال4: تابع

 را در نظر بگیرید.اگر X مجموعه تمام افراد مستطیع باشد، آنگاه تابع f  را تابع حج می‌نامیم که در آن عدد یک به منزله وجوب حج و عدد صفر به معنای عدم وجوب حج است.

خداوند متعال در قرآن کریم می‌فرمایند:

«وَلِلَّهِ عَلَى النَّاسِ حِجُّ الْبَیتِ مَنِ اسْتَطَاعَ إِلَیهِ سَبِیلًا[18]؛ و برای خدا برمردم است که آهنگ خانه (او) کنند، آن‌ها که توانایی رفتن به سوی آن دارند.»

تابع نمایی و لگاریتمی: تابع y=ax  که a>∘,a≠1  را تابع نمایی کلی گویند که در حالت خاص می‌توان به تابع y=ex  اشاره نمود (عدد e همان عدد نپر است که تقریباً مقدار آن 71/2 است). معکوس تابع اخیر را تابع لگاریتم طبیعی گویند و با y=ln(x)  نشان می‌دهند.

مثال1: در سال 1960 یک گروه از متخصصان بررسی کردند که آیا یک شیء هنری شامل مواد آلی که در مقبره توتانخامون (یکی از فراعنه مصر) پیدا شده، در طول زمان سلطنتش ساخته شده یا متعلق به زمان ما قبل از آن است؟ می‌دانیم که این فرعون (بر اساس نظریه دونالد ردفورد[19]) در 1346 سال قبل از میلاد از دنیا رفته و 10 سال بر مصر حکومت کرده است. اگر این شیء در طول مدت سلطنت توتانخامون ساخته شده باشد، چند درصد از میزان کربن 14 مشمول در شیء باید در سال 1960 موجود باشد ؟

پاسخ: نیمه عمر کربن 14 تقریبا 5700 سال است، بنابراین چون A(t)=A∘ekt  داریم:

A(57∘∘)=A∘e57∘∘k→12A∘=A∘e57∘∘k

پس داریم:

12=e57∘∘k→ln(12)=57∘∘k→k=ln(12)57∘∘~-∘/∘∘∘1216

با جایگذاری این مقدار در معادله داریم:

A(t)=A∘e-∘/∘∘∘1216t

زمان t سپری شده بین مرگ توتانخامون و سال 1960 میلادی برابر با t=196∘+1346=33∘6  است در این صورت داریم:

A(33∘6)=A∘e-∘/∘∘∘1216(33∘6)~∘/66897A∘

درصد میزان اصلی کربن 14 باقیمانده در شیء بعد ار 3306 سال 897/66 درصد است.

این فرعون، 10 سال بر مصر حکومت کرد، زمان سپری شده از آغاز سلطنت او تا سال 1960 برابر با 3316 = 10 + 3306 بوده است.

بنابراین:

 A(3316)=A∘e-∘/∘∘∘1216(3316)~∘/66816A∘

در این صورت اگر شیء هنری در طول مدت سلطنت توتانخامون ساخته شده باشد، باید میزان کربن14 باقیمانده آن در سال 1960 بین816/66 و 897/66 درصد باشد.

فراعنه سلسله‌ای از پادشاهان مصر بودند که بعضاً ادعای خدایی داشتند و برای ساختن قصرها و اهرام (که مقبره آن‌ها بود) افراد بسیاری در این راه کشته می‌شدند، اکنون می‌بینیم که فرعونی مانند توتانخامون ده سال حکومت کرد و قرن‌هاست نامی از او نیست و فقط باید پاسخگوی اعمالی باشد که انجام داده است. آیا عاقلانه است برای چند سال خوشگذرانی عذاب بی‌نهایت برای خود خرید؟! 

اکنون بدن مومیایی شده فراعنه درس عبرتی برای انسان‌هاست؛ خداوند در قرآن در مورد فرعون زمان حضرت موسی A می‌فرماید: «فَالْیوْمَ نُنَجِّیكَ بِبَدَنِكَ لِتَكُونَ لِمَنْ خَلْفَكَ آیةً وَ إِنَّ كَثِیرًا مِنَ النَّاسِ عَنْ آیاتِنَا لَغَافِلُونَ؛ [20]  ما امروز بدن تو را نجات می‌دهیم تا نشانه‌ای (و عبرتی) برای آیندگان باشی، و قطعاً بسیاری از مردم از نشانه‌های ما بی‌خبرند.»

مثال2: تابع نمایی را در مباحث اقتصادی نیز می‌توان به کار برد. به عنوان مثال مضاربه عبارت است از عقد خاصی بین دو نفر بدین صورت که سرمایه از یک طرف معین و کار از دیگری باشد و سود بین آن دو به نسبتی که قرار می‌گذارند، تقسیم می‌گردد. در مضاربه باید طرفین بالغ، عاقل و مختار باشند و مالک شرعا محجور (ممنوع التّصرف در مال ) نباشد. [21]

موجودی نهایی یک معامله که دارای سود مضاربه است می‌تواند بر مبنای فرمول زیر محاسبه شود:

F(x)=P(1+r)x

که در آن P موجودی اولیه و Fموجودی نهایی و r نرخ سود در هر دوره زمانی و x تعداد دوره‌های زمانی است. به عنوان مثال با استفاده از فرمول فوق می‌توان گفت که با نرخ سود 10 درصد چند دوره طول می‌کشد تا 100000 ریال تبدیل به 133100ریال شود.

x=ln(FP)ln(1+r)=ln(1331∘∘1∘∘∘∘∘)ln(1+∘/1)=∘/28593∘5394∘/∘9531∘1798∘~3

توابع مثلثاتی

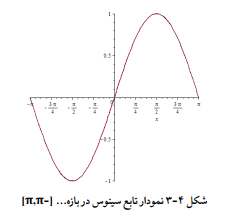
تعریف تابع سینوس: تابع سینوس را به صورت

y=sin(x)

نشان می‌دهیم که دامنه آن مجموعه اعداد حقیقی و برد آن [-1,1]  است نمودار تابع سینوس در شکل4-3 مشاهده می‌شود:

یکی از کارهای غیاث الدین جمشید کاشانی محاسبه سینوس (جیب[22]) زاویه یک درجه است[23] که این محاسبه با استفاده از روش ابتکاری حل یک معادله درجه سوم

sin3φ=3sinφ-4sin3φ

انجام گرفته است. لازم به ذکر است که هفده رقم اعشاری عدد به دست آمده با مقداری که امروزه محاسبه می‌شود همخوانی دارد.

مقدار سینوس یک درجه عدد  sin1=∘/∘174524∘643728351∘3712  است.

نمودار تابع سینوس همانطور که در شکل مشاهده می‌شود، در فاصله به طول 2π  بیشترین و کمترین مقدار خود را می‌گیرد که به این فاصله  دوره تناوب تابع سینوس می‌گوییم.

گریز:

رفتار بعضی از افراد نیز شبیه رفتار تابع سینوس است از جمله این افراد می‌توان به شَبَث ابن رِبعی اشاره نمود:

فرمانده نیروهاى پیادۀ عمر سعد در كربلا. وى از طایفۀ بنى تمیم و از جمله كسانى بود كه به حسین بن علىA نامه براى آمدن به كوفه نوشته بود. گرچه وى از چهره‌هاى معروف كوفه و در ابتدا از یاران علىA بود و حضرت او را همراه «عدىّ بن حاتم» نزد معاویه فرستاد و در جنگ صفّین هم در ركاب امیر المؤمنین بود، لیكن در مسیر حركت به سوى نهروان، همراه چند نفر دیگر سر از اطاعت آن حضرت بازتافتند و به خوارج پیوستند. علىA از آینده او خبر داده بود و به او و عمرو بن حریث فرمود: به خدا قسم شما دو نفر با فرزندم حسینA خواهید جنگید. روز عاشورا نیز امام حسینA در اوّلین سخنرانى مفصّل خویش خطاب به كوفیان از او هم نام برد و در اتمام حجّتى كه با آنان داشت و سخنان او را قطع مى‌كردند و گوش نمى‌دادند، از جمله فرمود:

«اى شبث بن ربعى و... مگر شما به من ننوشتید كه میوه‌ها رسیده و اطراف سر سبز است، اگر بیایى لشكریانى مجهّز براى تو آماده است؟»[24]

«شبث بن ربعى از چهره‌هاى متلوّن تاریخ بود. هم در قتل حسین بن علىA شركت داشت و پس از عاشورا مسجدى در كوفه تجدید بنا كرد، به شكرانه و خوش‌حالى از كشته شدن حسینA سپس همراه مختار، به خونخواهى حسین بن علىA پرداخت و رئیس پلیس مختار شد، سپس در كشتن مختار هم حضور داشت. پیشتر نیز با سجاح(مدعى دروغین نبوّت) همكارى داشت، مسلمان شد، بر ضدّ عثمان شورید، توبه كرد و از خوارج شد. به جاى بیعت با علىA با یك سوسمار بیعت كرد و مى‌گفت با هم برابرند! این مرد بددل و خبیث سرانجام در سن 80 سالگی در کوفه درگذشت»[25].

[1]ـ بهانه‌های عمر سعد در مقابل ولی خدا، حضرت اباعبدالله الحسین و نهایتاً بی‌ادبی در محضر ایشان

[2]ـ قال امام موسی کاظم A: «مَنِ اسْتَوی یوْماهُ فَهُوَ مَغْبُونٌ» (بحارالانوار، ج 78، ص 327).

[3]ـ نساء آیه  10.

[4]ـ سبا آیه  33.

 [5]ـ آل‌عمران آیه  185.

[6]ـ استاد در اینجا می‌تواند در صورتی که شرایط رامناسب ببیند، به حدیث شریف «حاسبوا قبل ان تحاسبوا» (به حساب خود برسید قبل از آن که به حساب شما رسیده شود) اشاره کند.

[7]ـ «واعْلَم أنَّ درجاتِ الجَنَّةِ على عَدَدِ آیات القرآن، فَإذا كانَ یوْمُ القِیامَةِ یقال لِقارِئ القرآن: اقْرَأ وارْقَ‏، فَلا یكونُ فی الجَنَّةِ بَعْد النَّبیینَ والصِّدِّیقینَ أرفع دَرجَةً مِنْهُ» (من لا یحضره الفقیه، ج2، ص627، ح 3215).

... درجات بهشت به شماره آیه‏هاى قرآنى است، و به كسى كه قرآن را تلاوت مى‏كند گویند: بخوان‏ و بالا برو...

[8]ـ خداوند به حضرت موسی (ع) فرمود ذکر باعث ترفیع درجات است (نصایح، ص110).

[9]- طه، آیه 114.

[10]-«مَنْ لَمْ يُصَلِّهِنَّ لِمَوَاقِيتِهِنَّ وَ لَمْ يُحَافِظْ عَلَيْهِنَّ فَذَاكَ إِلَيْهِ إِنْ شَاءَ غَفَرَ لَهُ وَ إِنْ شَاءَ عَذَّبَهُ» (کافی، ج3، ص268).

[11]ـ «إِنَّ الصَّلَاةَ إِذَا ارْتَفَعَتْ فِي أَوَّلِ وَقْتِهَا رَجَعَتْ إِلَى صَاحِبِهَا وَ هِيَ بَيْضَاءُ مُشْرِقَةٌ تَقُولُ حَفِظْتَنِي حَفِظَكَ اللَّهُ وَ إِذَا ارْتَفَعَتْ فِي غَيْرِ وَقْتِهَا بِغَيْرِ حُدُودِهَا رَجَعَتْ إِلَى صَاحِبِهَا وَ هِيَ سَوْدَاءُ مُظْلِمَةٌ تَقُولُ ضَيَّعْتَنِي ضَيَّعَكَ اللَّهُ» (الکافی، ج3، ص268).

[12]ـ «لَيْسَ مِنِّي مَنِ اسْتَخَفَّ بِصَلَاتِهِ لَا يَرِدُ عَلَيَّ الْحَوْضَ لَا وَ اللَّهِ لَيْسَ مِنِّي مَنْ يَشْرَبُ مُسْكِراً لَا يَرِدُ عَلَيَّ الْحَوْضَ لَا وَ اللَّهِ» (وسائل الشیعه، ج4، ص25).

[13]ـ توضیح المسائل آیت الله سیستانی، مساله 1369.

[14]ـ واقعه آیه  7- 11.

[15]ـ با توجه به تصریح آیه، چنین در نظر گرفته شده است که این سه گروه اشتراک ندارند.

[16]ـ واقعه آیه  88 - 94.

[17]ـ تفسیر المیزان ، ج19، ص 197.

[18]ـ آل عمران آیه   97.

[19]- Redford, D. B. (2003). The Oxford essential guide to Egyptian mythology.

[20]- یونس آیه  92.

[21]-توضیح المسائل مراجع، ج 2، ص263.

[22]ـ جیب بر وزن غیب.

 [23]ـ نقش غیاث الدین جمشید کاشانی در آموزش ریاضیات و ریاضیات محاسباتی، صص145ـ114.

[24]-«... یا شبث بن ربعى و یا... أ لم تكتبوا الىّ ان قد أینعت الثّمار و اخضرّ الجناب و انّما تقدم على جند لك مجنّدة؟... ؛ »(فرهنگ عاشورا، ج1، ص241)

[25]ـ همان .