نمونه 12- مطلب درسی: کاربرد انتگرال معین
1401/09/29 14:12فصل قبل
محاسبۀ مساحت ناحیه بین دو تابع:
اگر تابع f(x) و g(x)
روی بازه بسته [a,b]
پیوسته باشند، آنگاه مساحت ناحیه محصور بین دو تابعf(x)
و g(x)
و خطوط x=a
و x=b
برابر است با S=ab|f(x)-g(x)|dx
.
مثال1: اگر در یکی از روستاهای استان فارس سطح زیر کشت گندم به صورت ناحیه محدود به توابع f(x)=x2+4 و g(x)=5x
باشد و در هر هکتار، سه تن گندم به دست آمده باشد، چه میزان از محصول باید به عنوان زکات پرداخت شود.
پاسخ: زمین به صورت ناحیهای از بالا محدود به خط y=5x و از پایین محدود به منحنی y=x2+4
است و محدوده تغییرات x آن از 1 تا 4 (بر حسب 100 متر) است. بنابراین مساحت این زمین به صورت زیر محاسبه میشود:
A=14(5x-x2-4)dx=5x22-x33-4x&4&1=4/5
پس میزان محصول 13500 کیلوگرم است. با توجه به این که میزان محصول بیش از حد نصاب، 207/847 کیلوگرم است، زکات به محصول تعلق میگیرد. اگر کشت به صورت آبی باشد، یک بیستم (5 درصد) از محصول یعنی 675 کیلوگرم و اگر کشت به صورت دیم باشد دو برابر این میزان، یعنی 1350 کیلوگرم باید به عنوان زکات پرداخت شود.
مثال2: تابع حقیقی با ضابطه x>∘,y=1x را در نظر میگیریم و نمودار آن را در صفحه محورهای مختصات مانند شکل 4-11 رسم میکنیم.
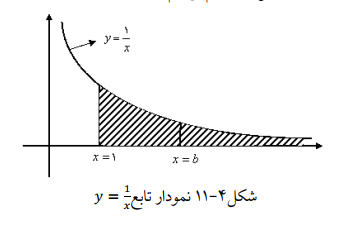
مرحلهی اول: سطح زیر منحنی به معادله y=1x,x>1 و محدود به محور x ها و خط x=1
طبق رابطه زیر به دست میآید.
A=limb→∞1b1xdx=limb→∞(lnx)&b&1=limb→∞(lnb-ln1)=limb→∞(lnb)=+∞ سطح
پس مقدار سطح A نامتناهی است و اگر بخواهیم این سطح را رنگ بزنیم، با تمام رنگهای دنیا هم نمیتوان این کار را انجام داد.
مرحله دوم: ما در این مرحله سطح نامتناهی A را حول محور xها دوران میدهیم. جسمی که از این دوران به دست میآید را اصطلاحاً «شیپور گابریل» میگویند. (شکل 4-12 را ببینید).
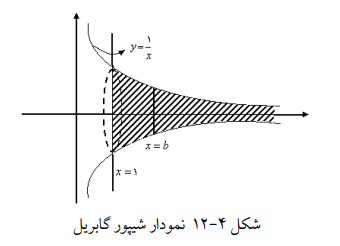
حجم شیپور گابریل به صورت زیر محاسبه میشود:
V=limb →∞π1by2 dx = limb →∞π1b1x2dx = limb →∞π (-1x)|1b= limb →∞π (-1b+1) =π
این محاسبه نشان میدهد که این شیپور را با π واحد مکعب رنگ میتوان پر از رنگ کرد.
مرحله سوم: ما در این مرحله این جسم را با صفحه محورهای مختصات برش عرضی میزنیم. مسلماً با توجه به محاسبه مرحلهی دوم برای رنگ آمیزی این مقطع به مقداری کمتر از π واحد مکعب رنگ احتیاج داریم. از طرفی این سطح مقطع دو برابر سطح نا متناهی A است، پس با توجه به مرحله اول حتی با تمام رنگهای دنیا هم نمیتوان این سطح مقطع را رنگآمیزی کرد.
گریز: در مقابل این سؤال که چگونه حجمی متناهی از اعمال، پاداش و جزایی نامتناهی[1] خواهد داشت؛ میتوان نمونههایی در ریاضی یافت. پارادوکس شیپور گابریل که در مثال بالا ذکرشده، یکی از این نمونههاست.
[1]ـ منظور از نامتناهی بودن پاداش این است که پاداش بهشتی پایان ناپذیر است. همانگونه که گاهی جزای جهنم نامتناهی است.