نمونه 8- مطلب درسی: حد تابع
1401/09/29 14:06فصل قبل
مفهوم حد در ریاضی را میتوان با این مثال توضیح داد:
رشته اعداد 1,12,14,18,⋯ را در نظر بگیرید.این رشته اگر به همین ترتیب ادامه یابد به صفر نزدیک میشود ولی هیچ گاه به صفر نمیرسد. بنابراین اصطلاحاً میگوییم که صفر حد این رشته عدد است. اما مهمترین مسأله این است که موضوع حد به بیان رفتار تابع میپردازد و میتواند رفتار آن را در نقاط مختلف و یا در بینهایت هم ارزیابی کند. ما در دنیای واقعی با پدیدههای تقریبی زیادی سرو کار داریم مثلاً یک ماشین را در نظر بگیرید که قرار است در یک جاده هموار با سرعت ثابت 100 کیلومتر در ساعت حرکت کند، اما میدانیم که نمیتوان همواره سرعت را روی عدد 100 ثابت نگه داشت بلکه آنچه ما در هر لحظه خواهیم داشت یک عدد تقریبی نزدیک به 100 است. در این صورت میتوانیم بگوییم سرعت ماشین ما به عدد 100 متمایل است. در واقع حد، بررسی رفتار یک تابع در اطراف و نزدیک به یک نقطه معین است.
گریز:
خداوند در قرآن کریم میفرماید:
«... وَالَّذِینَ آمَنُوا أَشَدُّ حُبًّا لِلَّهِ؛ و اما آنها که ایمان دارند، عشقشان به خدا شدیدتر است... [1] »
بنا بر این اگر علاقه و محبت یک شخص به خداوند را به عنوان تابعی از میزان ایمان او در نظر بگیریم، هر چه این ایمان بیشتر شود محبت او نیز به خدا افزایش مییابد.
قضیه فشردگی: اگر توابع f(x) ، g(x)
و h(x)
به گونهای باشند که در یک بازه حول a داشته باشیم:
g(x)≤f(x)≤h(x),
همچنین limx→ag(x)=limx→ah(x)=L در این صورت داریم: limx→af(x)=L
.
گریز:
در روایات آمده است که یکی از شرایط استجابت دعا این است که دعایتان را با صلوات شروع و با صلوات نیز ختم کنید تا اینکه دعایتان بین دو دعای مقبول واقع شود و مستجاب گردد زیرا خداوند، کریمتر از آن است که اول و آخر دعا را اجابت کند و وسط آن را اجابت ننماید. حضرت صادق A فرمودند: هرگاه کسی از شما دست به دعا برداشت، پس دعایش را با صلوات آغاز نماید؛ زیرا صلوات بر پیامبر A، دعایی پذیرفته شده است و خدای متعال برتر از آن است که بخشی از دعا را قبول کرده و بخش دیگر از آن را ردّ نماید.[2] نکته قابل توجه این است که استجابت دعا به معنای اعطای خواسته انسانها نیست بلکه خداوند متعال براساس حکمتش به انسانها عطا میکند و خواستههای آنها را برآورده میکند.
مفهوم بینهایت:
بینهایت تعداد اعضای مجموعهای است که نامتناهی است و در حقیقت بینهایت یک علامت و نشانه است که معنای آن «فراتر از هر مقدار» میباشد.
کاربرد در ریاضی عمومی:
در ریاضی عمومی مفاهیمی مانند حد در بینهایت و حد بینهایت[3] مطرح میشود.
امروزه در بانکها برای پرداخت تسهیلات از عقود مختلفی استفاده میشود یکی از عقود متداول، عقد بیع مرابحه است. بیع مرابحه به معاملهای اطلاق میگردد که فروشنده با اعلام بهای کالای خریداری شده، آن را گرانتر از قیمت خرید بفروشد. مثلا شخصی کالایی را به صورت نقد به قیمت 100 میلیون ریال خریداری و بابت حمل و نقل و... 10 میلیون ریال هزینه کند و بعد به مشتری اعلام کند که این کالا را که به صورت نقد خریدهام برای من 110 میلیون ریال تمام شده و آن را به 120 میلیون ریال میفروشم. این عقد را، عقد مرابحه میگویند.
وقتی مشتری به بانک مراجعه کرد و برای خرید کالایی درخواست تسهیلات میکند، بانک مبلغ درخواستی را به مشتری میدهد تا نسبت به خرید آن کالا به وکالت از بانک اقدام کند. بعد از آنکه کالا خریداری شد و به مالکیت بانک درآمد، بانک آن را به قیمتی بیش از قیمت نقدی خریداری شده به صورت اقساط به مشتری میفروشد. ناگفته نماند پولی که به مشتری داده میشود وام (قرض) نیست بلکه تسهیلات (پولی برای خرید کالای مورد نیاز مشتری) است و آنچه مشتری بازپرداخت میکند، اقساط وام نیست بلکه اقساط کالایی است که خریده است.
در اینجا ابتدا به فرمولی که برای محاسبات در بانک به کار میرود اشاره میکنیم و سپس رفتار تابع را در بینهایت و نیز در حالت مجانبی بررسی میکنیم.
مثال 1: در بانکی برای محاسبه میزان اقساط ماهیانه تسهیلات، که تابعی بر حسب نرخ سود ماهیانه است، از فرمول زیر استفاده میکند:
a(r)=Ar(1+r)n(1+r)n-1
که در آن nتعداد اقساط به ماه، A میزان مبلغ تسهیلات و rنرخ سود ماهیانه است. اکنون با استفاده از فرمول فوق میزان مبلغ قسط ماهیانه برای وامی به مبلغ 100 میلیون تومان با بازپرداخت به مدت 36 ماه و نرخ سود سالیانه 18 درصد را بدست آورید.
پاسخ: با توجه به اینکه نرخ سود تسهیلات سالیانه 18 درصد است پس r=0.1812=0.015
. اکنون داریم:
a(0.015)=100000000×0.015×(1+0.015)36(1+0.015)36-1≈3615240
همچنین میتوان نمودار تابع میزان اقساط ماهیانه وام را برحسب نرخ سود تسهیلات ماهیانه به صورت زیر رسم نمود:
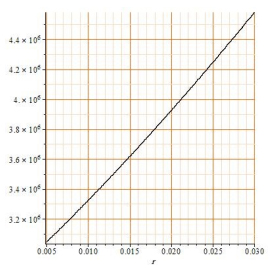
نکته: فرمولی که امروز برای محاسبه بازپرداخت این تسهیلات استفاده میشود به گونهای است که هر چه تعداد اقساط بیشتر شود میزان قسط کمتر است. البته به گونهای نیست که مبلغ قسط از مقدار معینی کمتر شود. این موضوع را با بررسی حد تابع وقتی تعداد اقساط به بینهایت میل میکند، میتوان دید.
مثال 2: در مثال فوق اگر برای دریافت همان میزان تسهیلات (100 میلیون تومان) و با همان نرخ سود سالیانه (18 درصد)، مدت زمان باز پرداخت مادامالعمر باشد، میزان مبلغ اقساط ماهیانه را بدست آورید.
پاسخ:
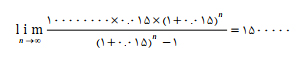
این مبلغ یعنی یک میلیون پانصد هزار تومان، کمترین مبلغ قسط برای تسهیلات صد میلیون تومان است.
نکته: اگر مبلغ قسط و میزان سود تسهیلات و تعداد اقساط مشخص باشد میتوان حداکثر مبلغ تسهیلات را مشخص کرد.
مثال 3: در بانکی برای محاسبه میزان مبلغ تسهیلات با مبلغ اقساط ماهیانه aتومان و با بازپرداخت n ماه که تابعی بر حسب نرخ سود ماهیانه r است، از فرمول زیر استفاده میکند:
A(r)=a((1+r)n-1)r(1+r)n
اکنون شخصی میخواهد تسهیلاتی از بانک بگیرد به گونهای که مبلغ اقساط ماهیانه آن مبلغ 500 هزار تومان و نرخ سود تسهیلات سالیانه 12 درصد و مدت زمان بازپرداخت 60 ماه باشد. مبلغ تسهیلاتی که این شخص میتواند از بانک دریافت کند، چقدر است؟
پاسخ: با توجه به اینکه نرخ سود تسهیلات سالیانه 12 درصد است پس r=0/1212=0/01
. اکنون داریم:
A(0/01)=500000((1+0/01)60-1)0/01(1+0/01)60=22477515
همچنین میتوان نمودار تابع مبلغ تسهیلات را بر حسب نرخ سود تسهیلات به صورت زیر رسم نمود:
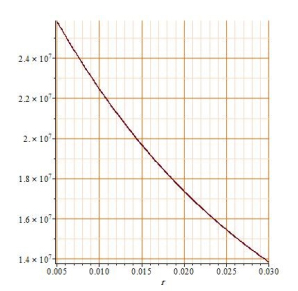
نکته: اگر مبلغ قسط و میزان سود تسهیلات و مبلغ تسهیلات مشخص باشد میتوان حداکثر تعداد اقساط را مشخص کرد.
مثال 4: در بانکی برای محاسبه مدت زمان بازپرداخت تسهیلاتی به مبلغ A و مبلغ اقساط a که تابعی بر حسب نرخ سود تسهیلات r است از فرمول زیر استفاده میکند:
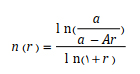
اکنون رئیس بانک تصمیم دارد به فردی به میزان 50 میلیون تومان و با مبلغ اقساط 1 میلیون تومان در ماه و با نرخ سود تسهیلات 4 درصد تسهیلات بدهد. مدت زمان باز پرداخت تسهیلات این فرد چند ماه میشود؟
پاسخ: با توجه به اینکه نرخ سود تسهیلات سالیانه 4 درصد است پسr=0.0412=0.0033
. اکنون داریم:
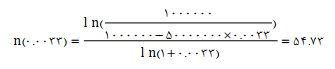
بنابراین حداقل مدت زمان باز پرداخت تسهیلات 55 ماه میشود.
همچنین میتوان نمودار تابع مدت زمان بازپرداخت اقساط تسهیلات را برحسب نرخ سود تسهیلات به صورت زیر رسم نمود:
حال به بررسی مشتق توابع مثالهای قبل نسبت به متغیر مربوطه میپردازیم:
مشتق a نسبت بهr در صورتی که A و n ثابت فرض شوند، به صورت زیر است:
dadr=A1+rn1+rn-1+ Ar1+rnn1+rn-1- Ar1+r2nn1+r1+rn-12
مشتق A نسبت به r در صورتی که a و n ثابت فرض شوند، به صورت زیر است:
dAdr=an(1+r)r-a((1+r)n-1)r2(1+r)n-a((1+r)n-1)nr(1+r)n(1+r)
اکنون اگر در رابطه nr=ln(aa-Ar)ln(1+r) ، a
و A
ثابت باشند داریم:
dndr=A(a-Ar)ln(1+r)-ln(aa-Ar))(1+r)(ln(1+r))2
اکنون اگر در رابطه A(n)=a((1+r)n-1)r(1+r)n r و aثابت باشند داریم:
dAdn=aln(1+r)r-a((1+r)n-1)ln(1+r)r(1+r)n
همچنین نمودار A نسبت به n به صورت زیر رسم میشود: (a=500000,r=0/01)
اکنون اگر در رابطهa(n)=Ar(1+r)n(1+r)n-1 مقادیر A و r ثابت باشند داریم
dadn=- Ar(1+r)2n ln(1+r)(1+rn-1)2
همچنین نمودار a نسبت به n به صورت زیر رسم میشود :
(A=100000000, r=0. 015)
اکنون اگر در رابطه n(A)=ln(aa-Ar)ln(1+r) مقادیر a و r ثابت باشند داریم:
dndA=r(a-Ar)ln(1+r)
همچنین نمودار n نسبت به A به صورت زیر رسم میشود: (a=1000000, r=0. 0033)
[1]ـ بقره آیه 165.
[2]ـ قال الصّادقُ A: «إذا دعا أحَدُکُم فَلْیَبْدَأ باِلصَّلاةِ علی النَّبیِّ صَلیَّ اللهُ علیه وآلهِ؛ فإنَّ الصَّلاةَ علی النَّبیِّ صَلیَّ اللهُ علیه وآله مَقْبُولَةٌ وَلَمْ یَکُن اللهُ لِیَقْبَلَ بَعضَ الدُّعاءِ وَیَرُدَّ بَعضا»ً (أمالی شیخ طوسی، ص172(
[3]ـ توجه به این نکته لازم است که برخی افراد فکر میکنند بینهایت بودن مجموعهها در ریاضی با بینهایت بودن خداوند یکی است در حالی که چنین نیست. بینهایت در ریاضی یک امر ذهنی است. اما در مورد خداوند «بی نهایت و نامحدود بودن» یک امر حقیقی است و به معنای آن است که علم، قدرت و حیات خداوند بینهایت است به این معنا که علم خداوند حدی ندارد و اینگونه نیست که مقداری از امور را میداند و مقداری از امور را نمیداند، بلکه همه چیز را میداند. همچنین قدرت و حیات خداوند حدی ندارد.