نمونه 13- مطلب درسی: دنباله و سری
1401/09/29 14:13فصل قبل
تعریف دنباله: منظور از یک دنباله، تابعی است که دامنۀ تعریف آن مجموعه اعداد طبیعی (با اضافه کردن عدد صفر) است. معمولاً به جای نوشتن f(n) از fn
یا an
استفاده میکنیم. an
را جمله عمومی دنباله گوییم.
مثال1: دنبالۀ an=1n که n=1,2,3,...
دارای جملاتی به صورت زیر است:
1,12,13,...
تعریف سری: فرض کنید دنباله {an} یک دنباله دلخواه است. دنباله جدید {sn}
را به صورت زیر میسازیم:
s1=a1;s2=a1+a2;s3=a1+a2+a3;...sn=a1+a2+a3+...an
به دنباله {sn} دنباله مجموع جزئی دنباله {an}
میگوییم، حد {sn}
را با نماد n=1∞an
نشان میدهیم و به آن سری میگوییم. سری را همگرا گوییم اگر حد دنباله{sn}
وجود داشته باشد و در غیر این صورت سری را واگرا گوییم.
یک سری میتواند متناهی و یا نامتناهی باشد. سریهای متناهی را میتوان با اعمال جبری محاسبه نمود ولی برای سریهای نامتناهی نمیتوان بدین صورت محاسبه را انجام داد. به عنوان مثال سری 1+2+3+...+n یک سری متناهی است که مجموع آن n(n+1)2
است. سری نامتناهی سری است که تعداد جملات آن نامحدود است. سری 1-1+1-1+...
یک سری نامتناهی است که واگراست و نمیتوان مجموع آن را حساب نمود اما سری 1+12+14+...
یک سری نامتناهی است که به آن سری هندسی با قدر نسبت 12
گویند و مجموع آن 2 است.
تعریف (همگرایی مطلق): گوییم سری n=1∞an «همگرای مطلق» است هرگاه سری n=1∞|an|
همگرا باشد.
نکته: سریای که همگرا هست اما همگرای مطلق نیست، «همگرای مشروط» گوییم. به عنوان مثال سری n=1∞(-1)nn یک سری همگرای مشروط است.
مثال2: روایت کردهاند که حکمران هند که به سختی تحت تأثیر اختراع بازی شطرنج قرار گرفته بود، به مخترع آن وعده داد که هر پاداشی بخواهد به او بدهد. مخترع تقاضایی کرد که به ظاهر خیلی ناچیز به نظر میرسید. او مقداری دانههای گندم در خواست کرد، به نحوی که اگر آنها را در خانههای صفحه شطرنج جا دهند، در هر خانه دو برابر خانه قبل وجود داشته باشد. به این ترتیب تعداد دانههای گندمی که او تقاضا کرد مساوی مجموع جملههای یک تصاعد هندسی بود که جمله اول آن ۱، قدر نسبتش ۲، و تعداد جملههایش مساوی ۶۴ بود. حکمران هند که ثروتمندترین مرد جهان بود، نتوانست از عهده این در خواست برآید. تعداد دانههای گندم برابر است با مجموع توانهای متوالی ۲ از ۰ تا ۶۳ یعنی: 18446744073709551615عدد گندم.
اگر در هر سانتیمتر مکعب ۲۰ دانه گندم قرار بگیرد، روی هم این تعداد گندم به اندازه 922337203685 متر مکعب فضا اشغال میکند (۲۰ میلیون گندم در هر متر مکعب). برای اینکه بتوان این مقدار گندم را بدست آورد باید هشت بار تمام زمین را کاشت و هشت بار محصول آنرا جمع کرد. به عبارت دیگر این محصول را از سیارهای میتوان بدست آورد که سطح آن هشت برابر زمین باشد. به این ترتیب مخترع شطرنج درس خوبی به حکمران هند داد و به او ثابت کرد که امکانات بی پایانی ندارد و نمیتواند «هر» خواهش مخترع را برآورد.
گریز: همچنانکه دانههای گندم در ظاهر تعداد کمی به نظر میرسند ولی در نهایت تعداد کل آنها رقم درشتی خواهد شد این موضوع در مورد گناهان نیز مصداق دارد. در واقع گناه ممکن است در ظاهر کوچک باشد ولی انجام مکرر گناهان کوچک میتواند در دراز مدت غیرقابل جبران شود. این را باید در نظر داشت كه وسوسههای شیطان یك مرتبه به انسان هجوم نمیآورد بلكه نوع وسوسههای شیطان از «سیاست گام به گام» پیروی میکند به این معنی كه شیطان به صورت كوچك جلوه دادن گناه در نظر شخص وی را قدم به قدم به سوی پرتگاه مذلت میکشاند.
«رسول خدا فرمود: بترسید از گناهانی كه آنها را كوچك شمارید كه آن قابل آمرزش نیست سؤال شد: كوچك شمردن گناه چیست؟ پیامبر اکرمJ فرمود: شخصی گناهی را مرتكب میشود سپس میگوید خوشا به حال من اگر غیر از این گناهی نداشته باشم». [1]
سری واگرا
گاهی در ریاضی برای ساخت شبهه از سری واگرا استفاده میشود که در واقع با محاسبات به ظاهر درست نتیجه نادرست به دست میآید.
در مثال زیر نمونهای مطرح در ریاضی را بیان میکنیم.
مثال 3: در عبارت پایین نشان داده شده است که ∘=1 در واقع داریم:
∘=(1-1)+(1-1)+...=1+(-1+1-1+1-...)=1+∘=1
نکتهای که در اثبات بالا نهفته است و باید به آن توجه کرد، جابجایی پرانتزهاست که مطلبی به ظاهر درست است. اما از آنجا که اگر سری، یك سری همگرای مطلق نباشد، نمیتوان آرایش جملات آن را عوض نمود، به نتیجهای نادرست دست یافتهایم. بنابراین در واقع تساوی بالا یک شبهه است تا یک حقیقت.
تعریف شبهه:
شاید در ابتدا این سؤال در ذهن مطرح شود که چرا به شک و گمان شبهه میگویند. در این باره امام علی (ع) میفرمایند: «شبهه را از این رو شبهه نامیدند زیرا که شباهت به حق دارد».[2]
همچنین میتوان گفت: شبهه، شروع با یک فرض درست، گنجاندن یک اشتباه در اثبات وگرفتن نتیجه غلط است.
سری همگرا (فیبوناچی)
مثال4: فرض کنید یک جفت خرگوش به شما داده شده که تازه به دنیا آمدهاند، یک ماه دیگر بالغ میشوند و دوران بارداری آنها نیز یک ماه طول میکشد و در هر بار زاد و ولد هم یک خرگوش نر و یک خرگوش ماده بدنیا میآورند. یعنی ماه اول و دوم شما یک جفت خرگوش دارید و ماه سوم یک جفت خرگوش دیگر به جفت قبلی اضافه میشود. در مورد ماه چهارم چه میتوان گفت؟
جفت اول یک جفت دیگر بدنیا میآورند و جفت دوم بعد از رسیدن به بلوغ در حال طی دوران بارداری هستند. پس در ماه چهارم سه جفت خرگوش خواهید داشت. در ماه پنجم جفت اول چهارمین جفت را بدنیا میآورد و جفت دوم پنجمین جفت را. یعنی در ماه پنجم پنج جفت خرگوش خواهید داشت. اگر محاسبات را به شرط این که خرگوشها هیچ وقت نمیرند، ادامه دهید و تعداد جفتهای خرگوش را در هر ماه پشت سر هم بنویسید به دنباله جالبی خواهید رسید :
...,1,1,2,3,5,8,13,21,34,55,89,144
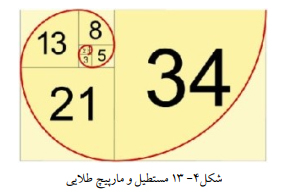
اولین نکتهای که از این دنباله نتیجه میشود این است که جمله اول و دوم آن عدد یک است و از جمله سوم به بعد هر جمله دنباله، جمع دو جمله قبلی است. اولین بار ریاضیدانی ایتالیایی بنام فیبوناچی این دنباله را در سال ۱۲۰۲ میلادی ارائه کرد که به همین خاطر به دنباله فیبوناچی معروف شده است.
نکته جالب در مورد دنباله فیبوناچی اینست که اگر هر جمله از این دنباله را به جمله قبلی تقسیم کنید دنباله جدیدی حاصل میشود که به عدد ثابت 1+52~1/618 همگراست که به عدد طلایی یا عدد فی معروف است.
چند تذکر:
در گریزها نباید به دنبال تطابق کامل آن با مبحث ریاضی بود بلکه فقط از آن برای انتقال از مطلب درسی به دینی بر اساس یک شباهت و تشبیه استفاده میشود.
بدون شک مدرسان علاوه برمثالهایی که در این فصل ذکر شد، مثالهای دیگری هم اضافه خواهند کرد اما لازم است به این نکته توجه شود که این امر حساسیت خاصی دارد و چه بسا مثالی در نگاه ابتدایی صحیح باشد اما با نگاه عمیق، نادرست بودن آن مشخص میشود. از اینرو اهمیت دارد مدرسان محترم قبل از ارایه مثالها در کلاس آن را با صاحب نظران، به بحث و تبادل نظر بگذارند.
در مباحث ریاضی که امروزه در دانشگاهها تدریس میشود، جای بررسی برخی مسائل شرعی خالی است. از جمله این مسائل شرعی میتوان به تعیین قبله، تعیین اوقات شرعی، محاسبه خمس، تعیین ابعاد مخزنی که حجم آب موجود در آن به اندازه آب کر باشد و محاسبه ارث نام برد. اگرچه در مباحث قبلی مثالهایی در خصوص برخی مسائل شرعی آورده شد اما پیشنهاد میشود، هماندیشی مناسبی بین فضلای حوزه علمیه و ریاضیدانان ایجاد شود.
[1]ـ «قَالَ أَبُو عَبْدِ اللَّهِ ع اتَّقُوا الْمُحَقَّرَاتِ مِنَ الذُّنُوبِ فَإِنَّهَا لَا تُغْفَرُ قُلْتُ وَ مَا الْمُحَقَّرَاتُ قَالَ الرَّجُلُ یذْنِبُ الذَّنْبَ فَیقُولُ طُوبَى لِی لَوْ لَمْ یكُنْ لِی غَیرُ ذَلِكَ» (الكافی، ج2، ص 287).
2- «إِنَّمَا سُمِّيَتِ الشُّبْهَةُ شُبْهَةً لِأَنَّهَا تُشْبِهُ الْحَق» (نهج البلاغه، خطبه 38، ص81)